CBSE Class 6 Math: Whole Numbers

Understanding Whole Numbers
Number Line Representation : Simulation
Comparing Whole Numbers : Simulation
Natural Numbers
Whole Numbers
Successor of a Whole Number
Predecessor of a Whole Number
Properties of Addition
Properties of Subtraction
Properties of Multiplication
Properties of Division
Whole Number Worksheet
Solutions

Understanding Whole Numbers

Whole numbers are a basic mathematical concept, forming the foundation for many more advanced topics. Let’s explore this concept step-by-step.

What are Whole Numbers?

Whole numbers are the numbers 0, 1, 2, 3, 4, 5, and so on.

They do not include fractions, decimals, or negative numbers.
They start from 0 and go on forever (infinite).

Examples of Whole Numbers:
0, 1, 2, 3, 4, 5, 100, 1000
Not Whole Numbers:
-5, 1.5, 3/4, √2

Properties of Whole Numbers

Closure Property
Whole numbers are closed under addition and multiplication.
This means if you add or multiply two whole numbers, the result will always be a whole number.
- Example: 4+5 = 9 (whole number)
- Example: 3×2 = 6 (whole number)
Commutative Property
Whole numbers follow the commutative property for both addition and multiplication.
This means you can change the order, and the result will remain the same.
- Addition: 4+5 = 5+4 = 9
- Multiplication: 3×2 = 2×3 = 6
Associative Property
Whole numbers also follow the associative property for addition and multiplication.
This means grouping numbers differently won’t change the result.
- Addition: (2+3)+4 = 2+(3+4) = 9
- Multiplication: (2×3)×4 = 2×(3×4) = 24
Additive Identity
Adding 0 to any whole number doesn’t change the number. 00 is called the additive identity.
- Example: 5+0 = 5
Multiplicative Identity
Multiplying any whole number by 1 doesn’t change the number. 11 is called the multiplicative identity.
- Example: 5×1 = 5
No Division Property
Whole numbers are not closed under division.
- Example: 4÷2 = 2 (whole number, okay)
- Example: 5÷2 = 2.5 (not a whole number)

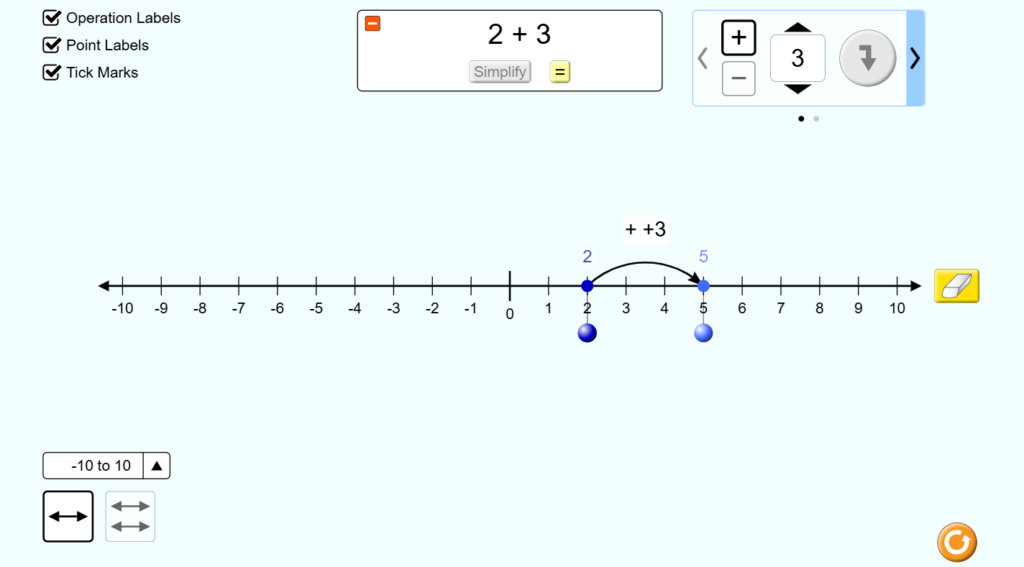
Number Line Representation

A number line is a simple way to visualize whole numbers.

Whole numbers are evenly spaced on the number line starting from 0.
Example: 0 --- 1 --- 2 --- 3 --- 4 --- 5 --- 6 --- ...

Using the Number Line:

To add two whole numbers, move right.

Example: 2+3: Start at 2, move 3 steps to the right, and land on 5.

Check how to Add and Subtract Whole Numbers visually using this SIMULATION

Click Here for Simulation

2. To subtract, move left.

Example: 5−2 : Start at 5, move 2 steps to the left, and land on 3.

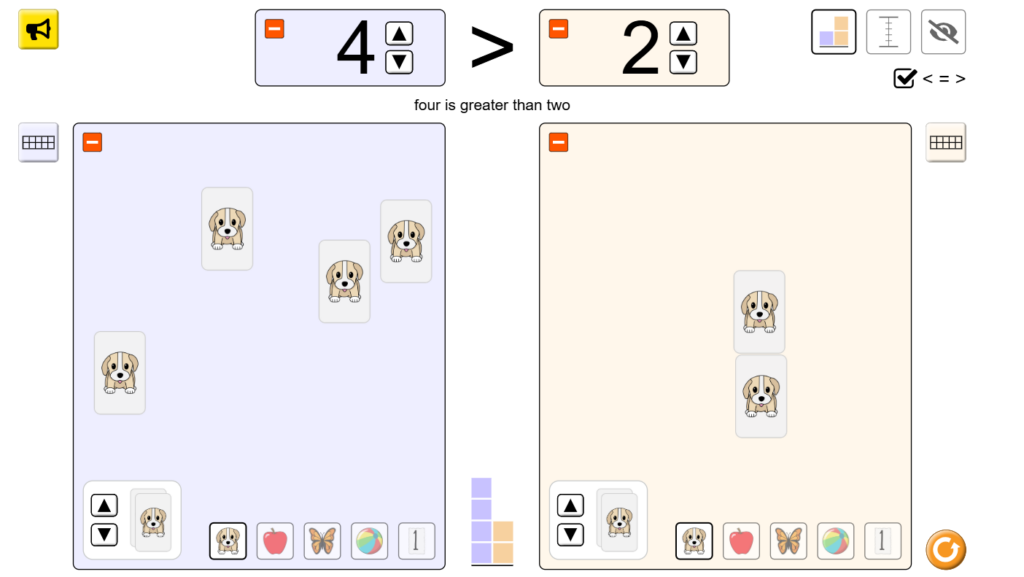
Comparing Whole Numbers

When comparing whole numbers:

Greater number is farther to the right on the number line.
Smaller number is farther to the left on the number line.

Examples:

5>2 (5 is greater than 2)
1<3 (1 is smaller than 3)

Check how to Compare Whole Numbers visually using this SIMULATION

Click Here for Simulation

Practical Examples

Counting Objects:
Whole numbers are used to count objects.
- Example: There are 5 apples on the table.
- Telling Age:
  Ages are whole numbers. You can’t say someone is 10.5 years old (unless adding decimals).
  - Example: A child is 10 years old.
- Money:
  When dealing with rupees or dollars in whole amounts.
  - Example: A pencil costs ₹15.

Quick Exercises

Identify whether the numbers are whole numbers:
- 7,−3,0,2.5,8
  (Answer: 7, 0, and 8 are whole numbers)
Use the number line to solve:
3+4 and 7−2.
Arrange these numbers in ascending order:
5,2,8,0,4
(Answer: 0, 2, 4, 5, 8)

Natural Numbers

Counting numbers, such as one, two, three, four, five, six, etc., are known as natural numbers.

1, 2, 3, 4, 5, 6, 7, 8, 9….

Whole Numbers

The natural numbers along with zero form the collection of whole numbers.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9…

1. All Natural numbers are whole numbers

2. All whole numbers are not natural numbers

Successor of a Whole Number

If we add 1 to a whole number then we get the next whole number, which is known as its successor. For example, successor of 0 is 1, successor of 1 is 2, and successor of 2 is 3.

Predecessor of a Whole Number

One less than a given whole number is known as its predecessor. For example, predecessor of 1 is 0, predecessor of 2 is 1 and predecessor of 3 is 2. Whole number 0 does not have it predecessor.

Properties of Addition

We have various properties of addition of whole numbers.

1. Closure property of addition

2. Commutative property of addition

3. Additive property of zero

4. Associative law of addition

Closure Property of Addition

If we add two whole numbers, then the result will be a whole number. Let us see some examples.

Example 1. Add 5 and 7, check if the sum is a whole number.

Solution. 5 + 7 = 12
12 is a whole number.

Example 2. Add 15 and 12, check if the sum is a whole number.

Solution. 15 + 12 = 27
27 is a whole number.

Commutative Property of Addition

If we add two whole numbers with different orders, then the sum will remain the same.

A + B = B + A
Let us see some examples.

Example 1. Check if 7 + 8 = 8 + 7.

Solution. 7 + 8 = 15 and 8 + 7 = 15
Thus, 7 + 8 is equal to 8 + 7.

Example 2. Check if 12 + 13 = 13 + 12.

Solution. 12 + 13 = 25 and 13 + 12 = 25
Thus, 12 + 13 is equal to 13 + 12.

Additive Property of Zero

Sum of any whole number and zero is the number itself.

5 + 0 = 0 + 5 = 5
12 + 0 = 0 + 12 = 12

Associative Law of Addition

In addition of whole numbers, the manner of associating the numbers does not affect the sum.

(a + b) + c = a + ( b + c)
Let’s consider some examples.

Example 1. Find the sum of 5, 8, 10.

Solution. (5 + 8) + 10 = 13 + 10 = 23
5 + (8 + 10) = 5 + 18 = 23
So, (5 + 8) + 10 = 5 + (8 + 10)

Properties of Subtraction

We have various properties of subtraction of whole numbers.

Property 1. If A and B are two whole numbers such that A > B or A = B, then A − B is a whole number. Otherwise, subtraction is not possible in whole numbers.

Property 2. If A and B are two whole numbers, then in general A − B is not equal to B − A.

Property 3. If A is any whole number, then A − 0 = A but 0 − A is not defined.

Property 4. If A, B, C are three whole numbers then, (A − B) − C is not equal to A − (B − C).

Properties of Multiplication

We have various properties of multiplication of whole numbers.

1. Closure property of multiplication

2. Commutative property of multiplication

3. Multiplicative property of zero

4. Multiplicative property of 1

5. Associative law of multiplication

6. Distributive law of multiplication over addition

7. Distributive law of multiplication over subtraction

Closure Property of Multiplication

If A and B are any two whole numbers, then product of A and B is also a whole number. Let’s see some examples.

Example 1. Product of 5 and 7.

Solution. 5 x 7 = 35
35 is a whole number

Example 2. Product of 8 and 11.

Solution. 8 x 11 = 88
88 is a whole number.

Commutative Property of Multiplication

If A and B are any two whole numbers, then A x B = B x A. Let’s see some examples.

Example 1. Check if 3 x 5 = 5 x 3.

Solution. 3 x 5 = 15 and 5 x 3 = 15
Thus 3 x 5 is equal to 5 x 3.

Example 2. Check if 5 x 15 = 15 x 5.

Solution. 5 x 15 = 75 and 15 x 5 = 75
Thus, 5 x 15 is equal to 15 x 5.

Multiplicative Property of Zero

Any whole number multiplied by zero gives the product zero.

5 x 0 = 0 x 5 = 0

Multiplicative Property of 1

Any whole number multiplied with 1 gives the number itself.

7 x 1 = 1 x 7 = 7

Associative Law of Multiplication

If A, B, C are any whole numbers then (A x B) x C = A x (B x C). Let’s see some examples.

Example 1. Multiply 4, 5 and 6.

Solution. 4 x 5 x 6 = (4 x 5) x 6 = 20 x 6 = 120
Changing the arrangement, we have:

4 x 5 x 6 = 4 x (5 x 6) = 4 x 30 = 120
Thus, (4 x 5) x 6 = 4 x (5 x 6)

Distributive Law of Multiplication Over Addition

If A, B, C are any whole numbers then A x (B + C) = A x B + A x C
Let’s see some examples.

Example 1. Check: 4 x (5 + 7) = 4 x 5 + 4 x 7

Solution. 4 x (5 + 7) = 4 x 12 = 48
And 4 x 5 + 4 x 7 = 20 + 28 = 48
Thus, 4 x (5 + 7) = 4 x 5 + 4 x 7.

Distributive Law of Multiplication Over Subtraction

If A, B, C are any whole numbers then A x (B − C) = A x B − A x C.

Let’s see some examples.

Example 1. Check: 5 x (6 − 2) = 5 x 6 − 5 x 2.

Solution. 5 x (6 − 2) = 5 x 4 = 20
And 5 x 6 − 5 x 2 = 30 − 10 = 20
Thus, 5 x (6 − 2) = 5 x 6 − 5 x 2.

Properties of Division

We have various properties of multiplication of whole numbers.

1. Division by zero

2. Zero divided by a natural number

Division by zero

If A and B are whole numbers, then A ÷ B is not always a whole number.

Let us consider 5 ÷ 0. Hence, we must find a whole number which when multiplied by zero gives 5. We are sure that no such number can be obtained.
Hence, we conclude that division by zero is not defined.

Zero Divided by a Natural Number

If we divide zero by any natural number, the result will be zero.
Let’s take some examples,

0 ÷ 4 = 0,

0 ÷ 6 = 0,

0 ÷ 8 = 0.

Practice Worksheets

Click here : Whole Number Worksheets

By practicing these concepts, you’ll gain a solid understanding of whole numbers and how they apply to everyday life! 😊

Contents :